- quadratic equation
-
Math.an equation containing a single variable of degree 2. Its general form is ax2 + bx + c = 0, where x is the variable and a, b, and c are constants (a non-zero).[1680-90]
* * *
A more descriptive name is second-degree polynomial equation. Its standard form is ax2 + bx + c = 0, and its solution is given by the quadratic formula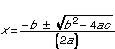 which guarantees two real-number solutions, one real-number solution, or two complex-number solutions, depending on whether the discriminate, b2 -4ac, is greater than, equal to, or less than 0.
which guarantees two real-number solutions, one real-number solution, or two complex-number solutions, depending on whether the discriminate, b2 -4ac, is greater than, equal to, or less than 0.* * *
in mathematics, an algebraic equation of the second degree (having one or more variables raised to the second power). Old Babylonian cuneiform texts, dating from the time of Hammurabi, show a knowledge of how to solve quadratic equations, but it appears that ancient Egyptian mathematicians did not know how to solve them. Since the time of Galileo, they have been important in the physics of accelerated motion, such as free fall in a vacuum. The general quadratic equation in one variable is ax2 + bx + c = 0, in which a, b, and c are arbitrary constants (or parameters) and a is not equal to 0. Such an equation has two roots (not necessarily distinct), as given by the quadratic formulaThe discriminant b2 − 4ac gives information concerning the nature of the roots (see discriminant). If, instead of equating the above to zero, the curve ax2 + bx + c = y is plotted, it is seen that the real roots are the x coordinates of the points at which the curve crosses the x-axis. The shape of this curve in Euclidean two-dimensional space is a parabola; in Euclidean three-dimensional space it is a parabolic cylindrical surface, or paraboloid.In two variables, the general quadratic equation is ax2 + bxy + cy2 + dx + ey + f = 0, in which a, b, c, d, e, and f are arbitrary constants and a, c ≠ 0. The discriminant (symbolized by the Greek letter delta, Δ) and the invariant (b2 − 4ac) together provide information as to the shape of the curve. The locus in Euclidean two-dimensional space of every general quadratic in two variables is a conic section or its degenerate.More general quadratic equations, in the variables x, y, and z, lead to generation (in Euclidean three-dimensional space) of surfaces known as the quadrics, or quadric surfaces.* * *
Universalium. 2010.
